An Internet packet generally includes two checksums: a TCP/UDP checksum and an IP checksum. In both cases, the checksum value is calculated using the same algorithm. For instance, IP header checksum is computed as follows:
- Set the packet’s IP header checksum to zero.
- Fetch the IP header octets in groups of 16-bit and calculate the accumulated sum.
- In case there’s an overflow while adding, sum the carry-bit to the total sum.
- Once the sum is done, set the checksum to the one’s complement of the accumulated sum.
Here is an implementation of such algorithm in Lua:
local ffi = require("ffi")
local bit = require("bit")
local function checksum_lua (data, size)
local function r16 (data)
return ffi.cast("uint16_t*", data)[0]
end
local csum = 0
local i = size
-- Accumulated sum.
while i > 1 do
local word = r16(data + (size - i))
csum = csum + word
i = i - 2
end
-- Handle odd sizes.
if i == 1 then
csum = csum + data[size-1]
end
-- Add accumulated carry.
while true do
local carry = bit.rshift(csum, 16)
if carry == 0 then break end
csum = bit.band(csum, 0xffff) + carry
end
-- One's complement.
return bit.band(bit.bnot(csum), 0xffff)
endThe IP header checksum is calculated only over the IP header octets. However, the TCP header is calculated over the TCP header, the packet’s payload plus an extra header called the pseudo-header.
A pseudo-header is a 12-byte data structured composed of:
- IP source and destination addresses (8 bytes).
- Protocol (TCP=0x6 or UDP=0x11) (2 bytes).
- TCP length, calculated from IP header’s total length minus TCP or UDP header size (2 bytes).
You may wonder what’s the purpose of the pseudo-header? David P Reed, often considered the father of UDP, provides a great explanation in this thread: Purpose of pseudo header in TCP checksum. Basically, the original goal of the pseudo-header was to take into account IP addresses as part of the TCP checksum, since they’re relevant fields in an end-to-end communication. Back in those days, the original plan for TCP safe communications was to leave source and destination addresses clear but encrypt the rest of the TCP fields. That would avoid man-in-the middle attacks. However NAT, which is essentially a man-in-the-middle, happened thrashing away this original plan. In summary, the pseudo-header exists today for legacy reasons.
Lastly, is worth mentioning that UDP checksum is optional in IPv4, so you might see it set as zero many times. However, the field is mandatory in IPv6.
Verifying a packet’s checksum
Verifying a packet’s checksum is easy. On receiving a packet, the receiver sums all the relevant octets, including the checksum field. The result must be zero if the packet is correct, since the sum of a number and its one’s complement is always zero.
From a developer’s perspective there are several tools for verifying the correctness of a packet’s checksum. Perhaps my preferred tool is Wireshark, which features an option to check the validity of TCP checksums (Edit->Preferences->Protocols[TCP]. Mark Validate the TCP checksum if possible). When this option is enabled, packets with a wrong checksum are highlighted in a black background.
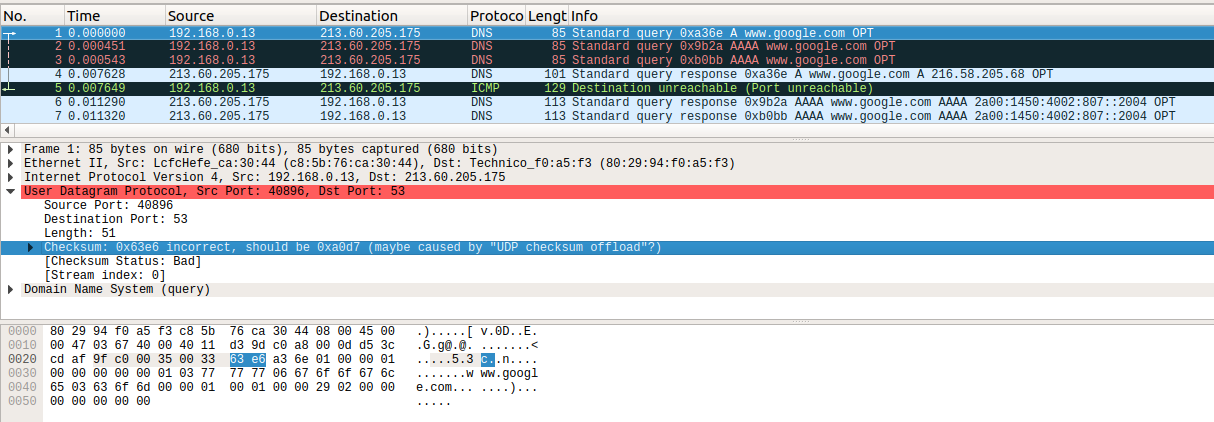
Seeing packets with wrong checksums is common when capturing packets with tcpdump and open them in Wireshark. The reason why checksums are not correct is that TCP checksumming is generally offloaded to the NIC, since it’s a relatively expensive operation (nowadays, NICs count with specialized hardware to do that operation fast). Since tcpdump captures outgoing packets before they hit the NIC, the checksum value hasn’t been calculated yet and likely contains garbage. It’s possible to check whether checksum offloading is enabled in a NIC by typing:
$ ethtool --show-offload <nic> | grep checksumming
rx-checksumming: on
tx-checksumming: onAnother option for verifying checksum values is using tshark:
$ tshark -r packets.pcap -V -o tcp.check_checksum:TRUE | grep -c "Error/Checksum"
20Lastly, in case you’d like to fix wrong checksums in a pcap file is possible to do that with tcprewrite:
$ tcprewrite -C -i packets.pcap -o packets-fixed.pcap
$ tshark -r packets-fixed.pcap -V -o tcp.check_checksum:TRUE | grep -c "Error/Checksum"
0Fast checksum computation
Since TCP checksum computation involves a large chunk of data improving its performance is important. There are, in fact, several RFCs dedicated exclusively to discuss this topic. RFC 1071 (Computing the Internet Checksum) includes a detailed explanation of the algorithm and also explores different techniques for speeding up checksumming. In addition, it features reference implementations in several hardware architectures such as Motorola 68020, Cray and IBM 370.
Perhaps the fastest way to recompute a checksum of a modified packet is to incrementally update the checksum as the packet gets modified. Take for instance the case of NAT which modifies origin and destination ports and addresses. Those operations affect both the TCP and IP checksums. In the case of the IP checksum, if the source address gets modified we can recompute the new IP checksum as:
new_checksum = ~(~checksum + (-pkt.source_ip) + new_source_ip);Or more generically using the following formula:
HC = one-complement(one-complement(C) + (-m) + m)This technique is covered in RFC 1071 and further polished over two other RFCs: RFC 1141 and RFC 1624 (Incremental Updating of the Internet Checksum).
If we decide to recompute the checksum, there are several techniques to do it fast. On its canonical form, the algorithm says octets are summed as 16-bit words. If there’s carry after an addition, the carry should be added to the accumulated sum. Truth is it’s not necessary to add octets as 16-bit words. Due to the associative property of addition, it is possible to do parallel addition using larger word sizes such as 32-bit or 64-bit words. In those cases the variable that stores the accumulative sum has to be bigger too. Once the sum is computed a final step folds the sum to a 16-bit word (adding carry if any).
Here’s an implementation in C using 32-bit words:
uint16_t checksum (uint8_t* data, uint16_t len)
{
uint64_t sum = 0;
uint32_t* p = (uint32_t*) data;
uint16_t i = 0;
while (len >= 4) {
sum = sum + p[i++];
len -= 4;
}
if (len >= 2) {
sum = sum + ((uint16_t*) data)[i * 4];
len -= 2;
}
if (len == 1) {
sum += data[len-1];
}
// Fold sum into 16-bit word.
while (sum>>16) {
sum = (sum & 0xffff) + (sum>>16);
}
return ntohs((uint16_t)~sum);
}Using larger word sizes increases speed as it reduces the total number of operations. What about using this technique on 64-bit integers? It definitely would be possible, but it requires to handle carry in the body loop. In the algorithm above, 32-bit words are summed to a 64-bit word. Carry, if any, is stored in the higher part of sum, which later gets summed in the folding step.
Using SIMD instructions should allow us to sum larger sizes of data in parallel. For instance using AVX2’s VPADD (vector-packed addition) instruction it should be possible to sum 16x16-bit words in parallel. The issue here once again is handling the possible generated carry to the accumulated sum. So instead of a 16x16-bit vector a 8x32 vector is used instead. From a functional point of view this is equivalent to sum using 128-bit words.
Snabb features implementations of checksum computation, generic and using SIMD instructions. In the latter case there are versions for SSE2 and AVX2 instruction sets. Snabb’s philosophy is to do everything in software and rely as much less as possible in offloaded NIC functions. Thus checksum computation is something done in code. Snabb’s implementation using AVX2 instructions is available at src/arch/avx2.c (Luke pushed a very interesting implementation in machine code as well. See PR#899).
Going back to RFC 1071, many of the reference implementations do additions in the main loop taking into account the carry bit. For instance, in the Motorola 68020 implementation that is done using the ADDXL instruction. In X86 there’s an equivalent add-with-carry instruction (ADC). Basically this instruction performs a sum of two operands plus the carry-flag.
Another technique described in RFC 1071, and also used in the reference implementations, is loop unrolling. Instead of summing one word per loop, we could sum 2, 4 or 8 words instead. A loop that sums 64-bit words in strides of 8 means actually avoiding loops for packet sizes lower than 512 bytes. Unrolling a loop requires adding waterfall code after the loop to handle the edge-cases that control the bounds of the loop.
As an exercise to teach myself more DynASM and X86-64 assembly, I decided to rewrite the generic checksum algorithm and see if performance improved. The first implementation followed the canonical algorithm, summing words as 16-bit values. Performance was much better than the generic Lua implementation posted at the beginning of this article, but it wasn’t better than Snabb’s C implementation, which does loop unrolling.
After this initially disappointing result, I decided to apply some of the optimization techniques commented before. Summing octets as 32-bit words definitely improved performance. The advantage of writing the algorithm in assembly is that I could make use of the ADC instruction. That allowed me to use 64-bit words. Performance improved once again. Finally I tried out several loop unrolling. With a loop unrolling of 4 strides the algorithm proved to be better than the SSE2 algorithm for several packet sizes: 64 bytes, 570 bytes and 1520 bytes. However, it doesn’t beat the AVX2 implementation in the large packet case, but it shown better performance for small and medium sizes.
And here’s the final implementation:
; Prologue.
push rbp
mov rbp, rsp
; Accumulative sum.
xor rax, rax ; Clear out rax. Stores accumulated sum.
xor r9, r9 ; Clear out r9. Stores value of array.
xor r8, r8 ; Clear out r8. Stores array index.
mov rcx, rsi ; Rsi (2nd argument; size). Assign rsi to rcx.
1:
cmp rcx, 32 ; If index is less than 16.
jl >2 ; Jump to branch '2'.
add rax, [rdi + r8] ; Sum acc with qword[0].
adc rax, [rdi + r8 + 8] ; Sum with carry qword[1].
adc rax, [rdi + r8 + 16] ; Sum with carry qword[2].
adc rax, [rdi + r8 + 24] ; Sum with carry qword[3]
adc rax, 0 ; Sum carry-bit into acc.
sub rcx, 32 ; Decrease index by 8.
add r8, 32 ; Jump two qwords.
jmp <1 ; Go to beginning of loop.
2:
cmp rcx, 16 ; If index is less than 16.
jl >3 ; Jump to branch '2'.
add rax, [rdi + r8] ; Sum acc with qword[0].
adc rax, [rdi + r8 + 8] ; Sum with carry qword[1].
adc rax, 0 ; Sum carry-bit into acc.
sub rcx, 16 ; Decrease index by 8.
add r8, 16 ; Jump two qwords.
3:
cmp rcx, 8 ; If index is less than 8.
jl >4 ; Jump to branch '2'.
add rax, [rdi + r8] ; Sum acc with qword[0].
adc rax, 0 ; Sum carry-bit into acc.
sub rcx, 8 ; Decrease index by 8.
add r8, 8 ; Next 64-bit.
4:
cmp rcx, 4 ; If index is less than 4.
jl >5 ; Jump to branch '3'.
mov r9d, dword [rdi + r8] ; Fetch 32-bit from data + r8 into r9d.
add rax, r9 ; Sum acc with r9. Accumulate carry.
sub rcx, 4 ; Decrease index by 4.
add r8, 4 ; Next 32-bit.
5:
cmp rcx, 2 ; If index is less than 2.
jl >6 ; Jump to branch '4'.
movzx r9, word [rdi + r8] ; Fetch 16-bit from data + r8 into r9.
add rax, r9 ; Sum acc with r9. Accumulate carry.
sub rcx, 2 ; Decrease index by 2.
add r8, 2 ; Next 16-bit.
6:
cmp rcx, 1 ; If index is less than 1.
jl >7 ; Jump to branch '5'.
movzx r9, byte [rdi + r8] ; Fetch 8-bit from data + r8 into r9.
add rax, r9 ; Sum acc with r9. Accumulate carry.
; Fold 64-bit into 16-bit.
7:
mov r9, rax ; Assign acc to r9.
shr r9, 32 ; Shift r9 32-bit. Stores higher part of acc.
and rax, 0x00000000ffffffff ; Clear out higher-part of rax. Stores lower part of acc.
add eax, r9d ; 32-bit sum of acc and r9.
adc eax, 0 ; Sum carry to acc.
mov r9d, eax ; Repeat for 16-bit.
shr r9d, 16
and eax, 0x0000ffff
add ax, r9w
adc ax, 0
; One's complement.
not rax ; One-complement of rax.
and rax, 0xffff ; Clear out higher part of rax.
; Epilogue.
mov rsp, rbp
pop rbp
; Return.
retBenchmark results for several data sizes:
Data size: 44 bytes
| Algorithm | Time per csum | Time per byte |
|---|---|---|
| Generic | 87.77 ns | 1.99 ns |
| SSE2 | 86.06 ns | 1.96 ns |
| AVX2 | 83.20 ns | 1.89 ns |
| New | 52.10 ns | 1.18 ns |
Data size: 550 bytes
| Algorithm | Time per csum | Time per byte |
|---|---|---|
| Generic | 1058.04 ns | 1.92 ns |
| SSE2 | 510.40 ns | 0.93 ns |
| AVX2 | 318.42 ns | 0.58 ns |
| New | 270.79 ns | 0.49 ns |
Data size: 1500 bytes
| Algorithm | Time per csum | Time per byte |
|---|---|---|
| Generic | 2910.10 ns | 1.94 ns |
| SSE2 | 991.04 ns | 0.66 ns |
| AVX2 | 664.98 ns | 0.44 ns |
| New | 743.88 ns | 0.50 ns |
All in all, it has been a fun exercise. I have learned quite a lot about the Internet checksum algorithm. I also learned how loop unrolling can help improving performance in a dramatic way (more than I initially expected). I found very interesting as well how changing the context of a problem, in this case the target programming language, forces to think about the problem in a different way but it also enables the possibility of doing more optimizations that were not possible before.
Update (17th November 2022):
Over the years I have been contacted about whether it would be possible to use the code of this post in other projects.
The algorithms in this post follow the same logic described in [RFC 1701] and follow-up RFCs, but adapted to larger word sizes (64 and 32 bit). There’s nothing novel about these algorithms. The RFCs already included reference implementations for different architectures.
So the answer is yes, you can use the code in this post for your projects. Referring this blog post is enough.
Projects using (or inspired by) the code of this post
- The x64 asm implementation was eventually merged into [Snabb] (https://github.com/snabbco/snabb/pull/1275).
- Sjors Hettinga took inspiration from this post to implement a faster checksum algorithm for the Zephyr RTOS
Please drop me a line if you have any feedback. Thanks!